티스토리 뷰
https://www.acmicpc.net/problem/1064
1064번: 평행사변형
평행사변형은 평행한 두 변을 가진 사각형이다. 세 개의 서로 다른 점이 주어진다. A(xA,yA), B(xB,yB), C(xC,yC) 이때, 적절히 점 D를 찾아서 네 점으로 평행사변형을 만들면 된다. 이때, D가 여러 개 나
www.acmicpc.net
분명히 쉬운문제인데.. 실수가 너무 잦아지고 있다. 집중해서 예외처리 하자.
문제 이해만 되면 쉬운 문제이다. 나는 예외처리에서 애먹었다.
문제 이해부터 해보자.
3개의 점으로 만들 수 있는 평행사변형은 총 3개이다. 예를 들어 다음과 같은 그림이 만들어진다.
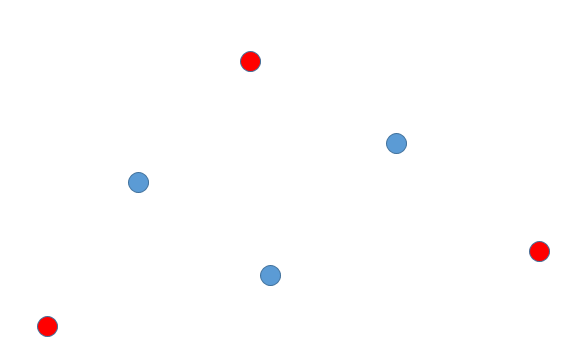
파란점이 주어진 점 3개이고, 빨간색 점으로 평행사변형을 만들 수 있다.
자. 이 사진을 보면 해법이 떠오르지 않는가?
문제는 만들어지는 모든 사각형 중 가장 큰 둘레 길이와 가장 작은 둘레 길이의 차이를 출력하는 것이다.
여기에서 둘레는 파란색 점으로 만들어지는 삼각형의 두 변의 두배와 같다. -> 생각해보거라..
그렇기 때문에 모든 사각형 중 가장 큰 둘레의 길이는 삼각형의 두 변의 합이 가장 큰 값이 되고, 가장 작은 둘레의 길이는 삼각형의 두 변의 합이 가장 작은 값이 된다.
이를 이용하여, 가장 큰 값과 가장 작은 값을 빼주면 답이 나오게 된다.
여기에서 예외처리를 해야할 것은 만들 수 있는 평행사변형이 없다면 -1을 출력하는 것이다.
여기에서 만들 수 있는 평행사변형이 없는 조건이 무엇이 될까?
평행사변형이 없는 조건은 한가지가 있지만 두가지가 있다.
왜 이런 이상한 말을 쓸까? 다음을 보고 알아보자
우선 평행사변형이 없는 조건으로 3개의 점이 한 직선 상에 존재하는 것이다. 그렇다면 3개의 점이 한 직선상에 있다는 것은 3점끼리의 기울기가 동일하다는 것을 알 수 있다.
여기에서 기울기를 구하기 위해 y1-y2 / x1 - x2의 조건을 많이 사용할 것이다. 여기에서 x1 = x2인 조건을 생각해야 한다.
이 때문에 조건은 한가지가 있지만 두가지가 있다고 말하였다. 나는 이 예외를 생각하지 못해 애먹었다 ㅠㅠ
그리고 이 두가지 조건을 하나의 코드로 끝낼 수 있다. 우선 내가 작성한 코드를 보여주겠다.
#include <cstdio>
#include <cmath>
int main(void) {
double x[3][2];
for (int i = 0; i < 3; i++) {
scanf("%lf", &x[i][0]);
scanf("%lf", &x[i][1]);
}
double length[3];
for (int i = 0; i < 3; i++) {
length[i] = sqrt(abs(pow(x[i][0] - x[(i + 1) % 3][0], 2) +
pow(x[i][1] - x[(i + 1) % 3][1], 2)));
}
if ((x[0][0] - x[1][0]) * (x[1][1] - x[2][1])
== (x[1][0] - x[2][0]) * (x[0][1] - x[1][1])) {
printf("-1");
return 0;
}
double max = length[0];
double min = length[0];
for (int i = 1; i < 3; i++) {
if (max < length[i]) max = length[i];
if (min > length[i]) min = length[i];
}
printf("%.12lf", 2*max - 2*min);
}여기 if문을 보면 원래 기울기를 구하는 공식은 y1 - y2 / x1 - x2인데, 여기에서 x1과 x2가 같을 경우 0이 나오게 된다. 그렇기 때문에 이것을 예외 처리해줘야 하지만, 이 코드는 y1 - y2 * x2 - x3 == y2 - y3 * x1 - x2를 해주어 0이 나오게 되는 상황도 없애주었다. 이렇게 생각을 조금만 더 해줘도 간단한 코드로 변형할 수 있다는 것을 알 수 있었다.
'코딩테스트 > Silver 5' 카테고리의 다른 글
| [S5] 1181. 단어 정렬 (1) | 2022.05.23 |
|---|---|
| [S5] 1094. 막대기 (0) | 2022.05.20 |
| [S5] 1059. 좋은 구간 (0) | 2022.05.19 |
| [S5] 1037. 약수 (0) | 2022.05.19 |
| [S5] 1018. 체스판 다시 칠하기 (0) | 2022.05.18 |
- Total
- Today
- Yesterday
- unistd.h
- bits/stdc++.h
- fastIo
- 행렬 멱법
- SCC 알고리즘
- 좌표 압축 알고리즘
- readString
- Witcher3
- ios::sync_with_stdio(false)
- deque와 vector의 차이
- 해시맵
- 에라토스테네스의 체
- 큰 수 계산
- 확장 유클리드
- tsp알고리즘
- readInt
- 분할정복
- scanf
- cin.tie(nullptr);
- 피보나치
- Set
- writeString
- writeInt
- 비트마스킹
- fread
- portal1
- manber myers
- 플로이드-워셜
- 트리보나치
- list
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
