티스토리 뷰
https://www.acmicpc.net/problem/10826
10826번: 피보나치 수 4
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
매우.. 오래걸렸다..
당연하게 쉬운 문제지만, 어렵게 풀어서 오래 걸렸다..
문제를 보면 입력되는 n의 수가 10,000보다 작거나 같은 자연수 또는 0이라고 나와있다. 나는 10,000번째의 피보나치 수를 검색해 보았다.
33644764876431783266621612005107543310302148460680063906564769974680081442166662368155595513633734025582065332680836159373734790483865268263040892463056431887354544369559827491606602099884183933864652731300088830269235673613135117579297437854413752130520504347701602264758318906527890855154366159582987279682987510631200575428783453215515103870818298969791613127856265033195487140214287532698187962046936097879900350962302291026368131493195275630227837628441540360584402572114334961180023091208287046088923962328835461505776583271252546093591128203925285393434620904245248929403901706233888991085841065183173360437470737908552631764325733993712871937587746897479926305837065742830161637408969178426378624212835258112820516370298089332099905707920064367426202389783111470054074998459250360633560933883831923386783056136435351892133279732908133732642652633989763922723407882928177953580570993691049175470808931841056146322338217465637321248226383092103297701648054726243842374862411453093812206564914032751086643394517512161526545361333111314042436854805106765843493523836959653428071768775328348234345557366719731392746273629108210679280784718035329131176778924659089938635459327894523777674406192240337638674004021330343297496902028328145933418826817683893072003634795623117103101291953169794607632737589253530772552375943788434504067715555779056450443016640119462580972216729758615026968443146952034614932291105970676243268515992834709891284706740862008587135016260312071903172086094081298321581077282076353186624611278245537208532365305775956430072517744315051539600905168603220349163222640885248852433158051534849622434848299380905070483482449327453732624567755879089187190803662058009594743150052402532709746995318770724376825907419939632265984147498193609285223945039707165443156421328157688908058783183404917434556270520223564846495196112460268313970975069382648706613264507665074611512677522748621598642530711298441182622661057163515069260029861704945425047491378115154139941550671256271197133252763631939606902895650288268608362241082050562430701794976171121233066073310059947366875
ㅋㅋ
보니까 2090글자가 나온다. 이것만 봐도 답이 나온다.
정수형으로는 절대 불가능.
그렇기 때문에 문자열을 이용하거나 bigInteger를 만들어 사용해야 한다.
나는 처음에는 쉬운 방법인 문자열을 이용해서 해결하였다. 그 코드는 다음과 같다.
#include <cstdio>
#include <iostream>
std::string stringSum(std::string a, std::string b) {
int c = 0;
std::string tmp;
for (int i = 0; i < a.length() || c != 0; i++) {
if (i < b.length()) {
tmp += ((c + a[i] - '0' + b[i] - '0') % 10) + '0';
c = (c + a[i] - '0' + b[i] - '0') / 10;
}
else if (i < a.length()) {
tmp += ((c + a[i] - '0') % 10) + '0';
c = (c + a[i] - '0') / 10;
}
else if (c != 0 && i >= a.length()) {
tmp += c + '0';
c = 0;
}
}
return tmp;
}
int main(void) {
std::string a = "1";
std::string b = "0";
std::string tmp;
int turn;
scanf("%d", &turn);
if (turn == 0) a = "0";
else if (turn == 1) a = "1";
for (int i = 2; i <= turn; i++) {
tmp = a;
a = stringSum(a, b);
b = tmp;
}
std::reverse(a.begin(), a.end());
std::cout << a;
}n이 10,000까지니까, O(n)으로 해도 시간이 크게 걸릴거 같지가 않았다. 하지만, 수가 커질수록 문자열에서 계산하는 +계산이 많아지기 때문에 약간 시간이 많이 나왔다. 그래서 그 문제를 해결하기 위해 저번에 피보나치와 관련한 문제에서 발견한 공식을 이용 + bigInteger클래스를 만들어 작성하려 한다.
[S5] 13301. 타일 장식물
https://www.acmicpc.net/problem/13301 13301번: 타일 장식물 대구 달성공원에 놀러 온 지수는 최근에 새로 만든 타일 장식물을 보게 되었다. 타일 장식물은 정사각형 타일을 붙여 만든 형태였는데, 한 변이
jhcard.tistory.com
우선 이 문제를 통해 피보나치 수를 O(logn)으로 계산할 수 있다는 것을 알고 와야 이해하기 편하다.
나는 피보나치와 관련한 문제는 13301번 문제에서 설명했기 때문에 해당 내용은 생략하고 오늘은 bigInteger와 관련한 내용을 설명하려 한다.
설명하기에 앞서 bigInteger를 이용한 코드를 소개하겠다.
#include <cstdio>
const int maxIdx = 300;
#define maxint 1000000000
class bigInt {
public:
int number[maxIdx];
int size;
bigInt(int n) {
number[0] = n;
for (int i = 1; i < maxIdx; i++) number[i] = 0;
this->size = 1;
}
bigInt() {
for (int i = 0; i < maxIdx; i++) number[i] = 0;
this->size = 1;
}
bigInt operator+(bigInt n) {
bigInt bigger = size > n.size ? *this : n;
bigInt smaller = size > n.size ? n : *this;
bigInt tmp(0);
int count = 0;
for (int i = 0; i < bigger.size || count != 0; i++) {
if (i < smaller.size) {
tmp.number[i] = (bigger.number[i] + count + smaller.number[i]) % maxint;
count = (bigger.number[i] + count + smaller.number[i]) / maxint;
}
else if (i < bigger.size) {
tmp.number[i] = (bigger.number[i] + count) % maxint;
count = (bigger.number[i] + count) / maxint;
}
else {
tmp.number[i] = count % maxint;
count = 0;
}
tmp.size = i + 1;
}
return tmp;
}
bigInt operator*(bigInt n) {
long long count = 0;
long long mulResult = 0;
bigInt result(0);
for (int i = 0; i < n.size; i++) {
for (int j = 0; j < size; j++) {
mulResult = (long long)n.number[i] * (long long)number[j] + (long long)result.number[i + j];
result.number[i + j] = mulResult % maxint;
count = mulResult / maxint;
int idx = i + j + 1;
if (result.size < idx) result.size = idx;
while (count) {
if (result.size < idx + 1) result.size = idx + 1;
long long qutio = (long long)result.number[idx] + count;
result.number[idx] = qutio % maxint;
count = qutio / maxint;
idx++;
}
}
}
return result;
}
void operator=(bigInt n) {
for (int i = 0; i < n.size; i++) number[i] = n.number[i];
size = n.size;
}
void print() {
if (size <= 0) { printf("%d", 0); return; }
printf("%d", number[size - 1]);
for (int i = size - 2; i >= 0; i--) {
for (int j = 0; j < 9 - digit(number[i]); j++) printf("0");
printf("%d", number[i]);
}
}
int digit(int num) {
int first = 10;
int count = 1;
while (num % first != num) {
count++;
first *= 10;
}
return count;
}
};
void calc(bigInt a[][2], bigInt b[][2]) {
bigInt tmp[2][2];
tmp[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
tmp[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
tmp[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
tmp[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
for (int i = 0; i < 2; i++) for (int j = 0; j < 2; j++) a[i][j] = tmp[i][j];
}
int main(void) {
int n;
scanf("%d", &n);
bigInt matrix[2][2] = { {1, 1}, {1, 0} };
bigInt result[2][2] = { {1, 0}, {0, 1} };
while (n) {
if (n % 2 == 1) {
n--;
calc(result, matrix);
if (n == 0) break;
}
n /= 2;
calc(matrix, matrix);
}
result[1][0].print();
}코드 수만 봐도 어지럽다. ㅋㅋㅋ
main함수를 먼저 보자. matrix 배열과 result배열은 13301번에 나온 방식과 똑같다. calc 함수만 보면 bigInt에 들어가야 할 요소들은 다음과 같다. bigInt에 저장할 숫자, bigInt끼리의 +계산과 *계산, print함수.
이것만 해결하면 끝난다.
그 부분이 bigInt클래스의 operator+, operator*부분에 해당한다.(print함수는 생략..)
지금 bigInt형의 number부분을 보면 int형의 배열로 구성되어있다. char형이 아니다. 신기방기?
자 그러니까 number의 한 원소에는 1,000,000,000까지의 수가 표현이 된다.
만약 7366719731392746273629108210679280이 수를 표현하고자 한다면 7366719731392746273629108210679280이렇게 나눠서 number의 배열에 들어가게 되는 것이다. 현재 number를 사용하고 있는 개수를 size에 저장을 하는 것이고, 이 size는 print함수에서 사용이 된다.(수를 표현해야 하니까(출력))
자 이제 bigInt에 저장되는 원소는 알았다. 이제 가장 중요한 부분이 남았다. +와 *계산이다.
우선 +먼저 해보자
operator+ 부분을 가져오면
bigInt operator+(bigInt n) {
bigInt bigger = size > n.size ? *this : n;
bigInt smaller = size > n.size ? n : *this;
bigInt tmp(0);
int count = 0;
for (int i = 0; i < bigger.size || count != 0; i++) {
if (i < smaller.size) {
tmp.number[i] = (bigger.number[i] + count + smaller.number[i]) % maxint;
count = (bigger.number[i] + count + smaller.number[i]) / maxint;
}
else if (i < bigger.size) {
tmp.number[i] = (bigger.number[i] + count) % maxint;
count = (bigger.number[i] + count) / maxint;
}
else {
tmp.number[i] = count % maxint;
count = 0;
}
tmp.size = i + 1;
}
return tmp;
}쉽다!
그러니까 bigInt끼리의 number가 있을 것이다. number의 같은 위치에 있는 수 끼리 더해주고, 더한 값이 1,000,000,000을 초과한다면 초과한 값을 1,000,000,000으로 나눠준 값이 올림 수로 들어가게 된다. 그 올림수는 더해준 number의 위치의 다음 위치에 들어가게 될 것이다.
이해가 되나? 여기에서 예외상황은 발생하지 않는다. 그러니까 int형이 오버플로우 될 걱정은 안해도 된다.(증명 생략)
다음으로 *계산이다. 살짝 이해하기 어려울 것이다. 나도 겨우 이해했..
bigInt operator*(bigInt n) {
long long count = 0;
long long mulResult = 0;
bigInt result(0);
for (int i = 0; i < n.size; i++) {
for (int j = 0; j < size; j++) {
mulResult = (long long)n.number[i] * (long long)number[j] + (long long)result.number[i + j];
result.number[i + j] = mulResult % maxint;
count = mulResult / maxint;
int idx = i + j + 1;
if (result.size < idx) result.size = idx;
while (count) {
if (result.size < idx + 1) result.size = idx + 1;
long long qutio = (long long)result.number[idx] + count;
result.number[idx] = qutio % maxint;
count = qutio / maxint;
idx++;
}
}
}
return result;
}그러니까 이거는 좀 복잡하다.
원리를 그림으로 설명하겠다.
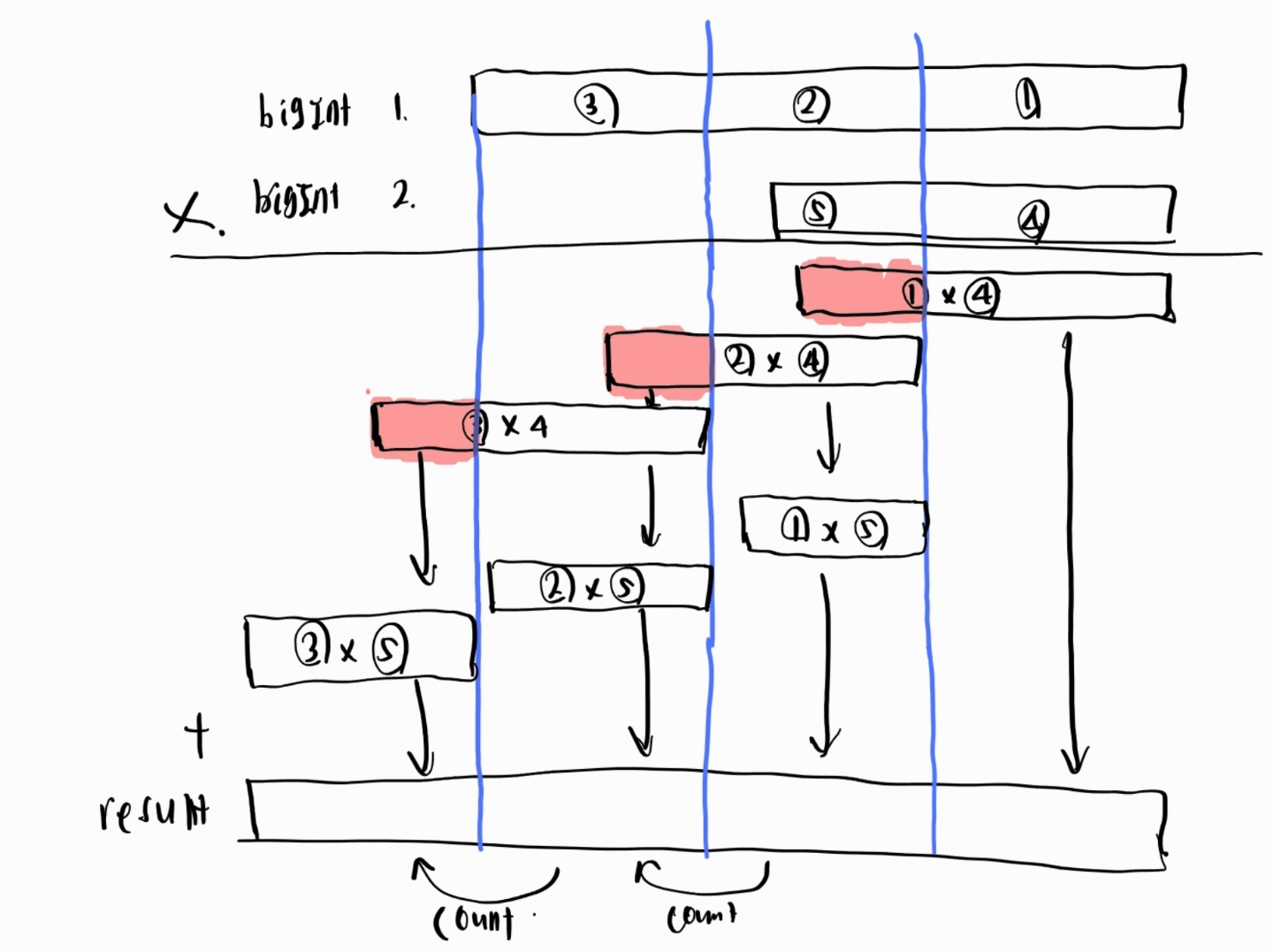
이런식으로 작동된다..
중간에 오류가 많았어서 코딩하는데 정말 오래걸린 코드이다 ㅠㅠ
'코딩테스트 > Silver 5' 카테고리의 다른 글
| [S5] 2161. 카드1 (0) | 2022.06.27 |
|---|---|
| [S5] 5555. 반지 (0) | 2022.06.26 |
| [S5] 2018. 수들의 합 5 (0) | 2022.06.24 |
| [S5] 2535. 아시아 정보올림피아드 (0) | 2022.06.24 |
| [S5] 13301. 타일 장식물 (0) | 2022.06.24 |
- Total
- Today
- Yesterday
- bits/stdc++.h
- Set
- 에라토스테네스의 체
- tsp알고리즘
- portal1
- writeInt
- unistd.h
- 행렬 멱법
- 큰 수 계산
- writeString
- readInt
- Witcher3
- 비트마스킹
- ios::sync_with_stdio(false)
- 좌표 압축 알고리즘
- 트리보나치
- cin.tie(nullptr);
- scanf
- fastIo
- 확장 유클리드
- manber myers
- 해시맵
- 플로이드-워셜
- readString
- list
- SCC 알고리즘
- 분할정복
- 피보나치
- deque와 vector의 차이
- fread
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
